segunda-feira, 7 de novembro de 2011
Exercícios com respostas.
1) Gráficos das funções f1(x)=3x, f2(x)=5x, f3(x)=7x, f4(x)=1 e f5(x)=0, estão traçados na figura abaixo.

Quais dos gráficos não são funções exponenciais?
Resposta:
As funções f4(x)=1 e f5(x)=0 são constantes e não são funções exponenciais.
______________________________________________
2) Construir em um mesmo plano cartesiano, um gráfico com as seguintes funções:
g1(x) = 3-x, g2(x) = 5-x e g3(x) = 7-x
Resposta:


Quais dos gráficos não são funções exponenciais?
Resposta:
As funções f4(x)=1 e f5(x)=0 são constantes e não são funções exponenciais.
______________________________________________
2) Construir em um mesmo plano cartesiano, um gráfico com as seguintes funções:
g1(x) = 3-x, g2(x) = 5-x e g3(x) = 7-x
Resposta:

O CRESCIMENTO POPULACIONAL
Em 1798, Thomas Malthus, no trabalho "An Essay on the Principle of Population" formulou um modelo para descrever a população presente em um ambiente em função do tempo. Considerou N=N(t) o número de indivíduos em certa população no instante t. Tomou as hipóteses que os nascimentos e mortes naquele ambiente eram proporcionais à população presente e a variação do tempo conhecida entre os dois períodos. Chegou à seguinte equação para descrever a população presente em um instante t:
N(t)=No ert
Onde No é a população presente no instante inicial t=0 e r é uma constante que varia com a espécie de população.
É evidente que o gráfico correto desta função depende dos valores de No e de r. Mas sendo uma função exponencial, a forma do gráfico será semelhante ao da função y=Kex.
Este modelo supõe que o meio ambiente tenha pouca ou nenhuma influência sobre a população. Desse modo, ele é mais um indicador do potencial de sobrevivência e de crescimento de cada espécie de população do que um modelo que mostre o que realmente ocorre.
Consideremos por exemplo uma população de bactérias em um certo ambiente. De acordo com esta equação se esta população duplicar a cada 20 minutos, dentro de dois dias, estaria formando uma camada em volta da terra de 30 cm de espessura. Assim, enquanto os efeitos do meio ambiente são nulos, a população obedece ao modelo N=Noer.t. Na realidade, quando N=N(t) aumenta, o meio ambiente oferece resistência ao seu crescimento e tende a mantê-lo sobre controle. Exemplos destes fatores são, a quantidade disponível de alimentos, acidentes, guerras, epidemias,...
Como aplicação numérica, consideremos uma colônia de bactérias se reproduzindo normalmente. Se num certo instante havia 200 bactérias na colônia, passadas 12 horas havia 600 bactérias. Quantas bactérias haverá na colônia após 36 horas da última contagem?
No instante inicial havia 200 bactérias, então No=200, após 12 horas havia 600 bactérias, então
N(12) = 600 = 200 er12
logo
e12r = 600/200 = 3
assim
ln(e12r) = ln(3)
logo
e12r = 600/200 = 3
assim
ln(e12r) = ln(3)
Como Ln e exp são funções inversas uma da outra, segue que:
12r = ln(3)
assim:
r = ln(3)/12 = 0,0915510
Assim:
N(48) = 200 e48.(0,0915510) = 16200 bactérias
assim:
r = ln(3)/12 = 0,0915510
Assim:
N(48) = 200 e48.(0,0915510) = 16200 bactérias
Então, após 36 horas da última contagem, ou seja, 48 horas do início da contagem, haverá 16200 bactérias.
CONCLUSÃO
Podemos dizer que as funções são utilizadas no nosso dia a dia. Em cálculos rotineiros como em juros, produtividade de uma empresa...
A função pode ser expressa graficamente, o que facilita a visualização do cálculo.
GRÁFICOS DA FUNÇÃO EXPONENCIAL
Função exponencial 0 < a < 1 | Função exponencial a > 1 |
f: lR x  ● Domínio = lR ● Contradomínio = lR+ ● f é injectiva ● f(x) > 0 , ⍱ x Є lR ● f é continua e diferenciável em lR ● A função é estritamente decrescente. ● limx→ -∞ ax = + ∞ ● limx→ +∞ ax = 0 ● y = 0 é assimptota horizontal | f: lR x  ● Domínio = lR ● Contradomínio = lR+ ● f é injectiva ● f(x) > 0 , ⍱ x Є lR ● f é continua e diferenciável em lR ● A função é estritamente crescente. ● limx→ +∞ ax = + ∞ ● limx→ -∞ ax = 0 ● y = 0 é assimptota horizontal |
História da função exponencial.
Como um termo matemático, "função" foi introduzido por Leibniz em 1694, para descrever quantidades relacionadas a uma curva; tais como a inclinação da curva ou um ponto específico da dita curva. Funções relacionadas à curvas são atualmente chamadas funções diferenciáveis e são ainda o tipo de funções mais encontrado por não-matemáticos. Para este tipo de funções, pode-se falar em limites e derivadas; ambos sendo medida da mudança nos valores de saída associados à variação dos valores de entrada, formando a base do cálculo infinitesimal.
A palavra função foi posteriormente usada por Euler em meados do século XVIII para descrever uma expressão envolvendo vários argumentos; i.e:y = F(x). Ampliando a definição de funções, os matemáticos foram capazes de estudar "estranhos" objetos matemáticos tais como funções que não são diferenciáveis em qualquer de seus pontos. Tais funções, inicialmente tidas como puramente imaginárias e chamadas genericamente de "monstros", foram já no final do século XX, identificadas como importantes para a construção de modelos físicos de fenômenos tais como o movimento Browniano.
Durante o Século XIX, os matemáticos começaram a formalizar todos os diferentes ramos da matemática. Weierstrass defendia que se construisse o cálculo infinitesimal sobre a Aritmética ao invés de sobre a Geometria, o que favorecia a definição de Euler em relação à de Leibniz (veja aritmetização da análise). Mais para o final do século, os matemáticos começaram a tentar formalizar toda a Matemática usando Teoria dos conjuntos, e eles conseguiram obter definições de todos os objetos matemáticos em termos do conceito de conjunto. Foi Dirichlet quem criou a definição "formal" de função moderna.
Explicação + Exemplo
A função exponencial mais simples é a função 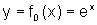 . Cada ponto do gráfico é da forma
. Cada ponto do gráfico é da forma 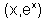 pois a ordenada é sempre o resultado de ex, ou seja, a exponencial de base e do número x.
pois a ordenada é sempre o resultado de ex, ou seja, a exponencial de base e do número x.
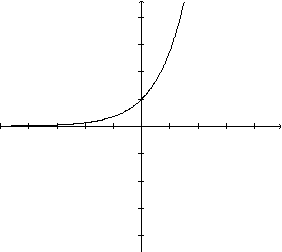
 Consideremos uma função exponencial cuja expressão é dada por
Consideremos uma função exponencial cuja expressão é dada por 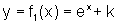 , onde k é uma constante real. A pergunta natural a ser feita é: qual a ação da constante k no gráfico dessa nova função quando comparado ao gráfico da função inicial
, onde k é uma constante real. A pergunta natural a ser feita é: qual a ação da constante k no gráfico dessa nova função quando comparado ao gráfico da função inicial 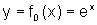 ?
? Vejamos qual o papel desempenhado por uma constante b, não nula , na função exponencial da forma
Vejamos qual o papel desempenhado por uma constante b, não nula , na função exponencial da forma 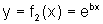 , quando a comparamos à função mais simples
, quando a comparamos à função mais simples 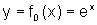 .
. Ainda podemos pensar numa função exponencial que seja dada pela expressão
Ainda podemos pensar numa função exponencial que seja dada pela expressão 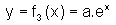 , onde a é uma contante real , a
, onde a é uma contante real , a 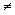 0
0 Uma questão que ainda se coloca é a consideração de funções exponenciais do tipo
Uma questão que ainda se coloca é a consideração de funções exponenciais do tipo 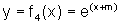 , onde m é um número real não nulo.
, onde m é um número real não nulo.
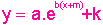
Conclusão: Podemos, portanto, considerar funções exponenciais do tipo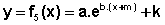 , onde os coeficientes a e b não são zero, examinando as transformações do gráfico da função mais simples
, onde os coeficientes a e b não são zero, examinando as transformações do gráfico da função mais simples 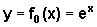 , quando fazemos, em primeiro lugar,
, quando fazemos, em primeiro lugar, 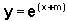 ; em seguida,
; em seguida, 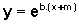 , depois
, depois 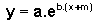 e, finalmente,
e, finalmente, 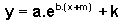 .
.
Analisemos o que aconteceu:
em primeiro lugar, 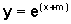 sofreu uma translação horizontal de -m unidades, pois x=-m exerce o papel que x=0 exercia em
sofreu uma translação horizontal de -m unidades, pois x=-m exerce o papel que x=0 exercia em 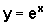 ;
;
em segundo lugar, em 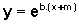 ocorreu mudança de inclinação, deixando fixo o ponto (-m,1) quando comparamos o gráfico com o anterior; essa mudança de inclinação foi provocada pelo fator b no expoente, que muda a base da função exponencial;
ocorreu mudança de inclinação, deixando fixo o ponto (-m,1) quando comparamos o gráfico com o anterior; essa mudança de inclinação foi provocada pelo fator b no expoente, que muda a base da função exponencial;
a seguir, no gráfico de 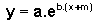 ocorreu mudança de inclinação pois, em cada ponto, a ordenada é igual àquela do ponto de mesma abscissa em
ocorreu mudança de inclinação pois, em cada ponto, a ordenada é igual àquela do ponto de mesma abscissa em 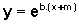 , multiplicada pelo coeficiente a;
, multiplicada pelo coeficiente a;
por fim, o gráfico de 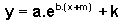 sofreu uma translação vertical de k unidades, pois, para cada abscissa, as ordenadas dos pontos do gráfico
sofreu uma translação vertical de k unidades, pois, para cada abscissa, as ordenadas dos pontos do gráfico 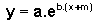
O estudo dos gráficos das funções envolvidas auxilia na resolução de equações ou inequações, pois as operações algébricas a serem realizadas adquirem um significado que é visível nos gráficos das funções esboçados no mesmo referencial cartesiano.
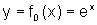 . Cada ponto do gráfico é da forma
. Cada ponto do gráfico é da forma 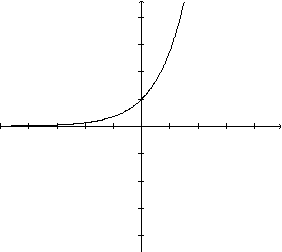
O domínio da função 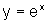 é
é 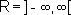 e a imagem é o conjunto
e a imagem é o conjunto 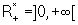 .
.
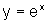 é
é 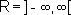 e a imagem é o conjunto
e a imagem é o conjunto 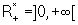 .
.O eixo horizontal é uma assíntota do gráfico da função. O que queremos aqui é descobrir como é o gráfico de uma função exponencial geral, quando comparado ao gráfico de 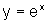 , a partir das transformações sofridas por esta função.
, a partir das transformações sofridas por esta função.
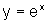 , a partir das transformações sofridas por esta função.
, a partir das transformações sofridas por esta função.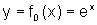 ?
?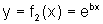 , quando a comparamos à função mais simples
, quando a comparamos à função mais simples 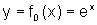 .
.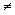 0
0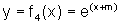 , onde m é um número real não nulo.
, onde m é um número real não nulo.CONCLUSÃO:
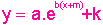
Conclusão: Podemos, portanto, considerar funções exponenciais do tipo
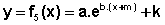 , onde os coeficientes a e b não são zero, examinando as transformações do gráfico da função mais simples
, onde os coeficientes a e b não são zero, examinando as transformações do gráfico da função mais simples 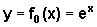 , quando fazemos, em primeiro lugar,
, quando fazemos, em primeiro lugar, 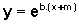 , depois
, depois 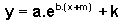 .
.Analisemos o que aconteceu:
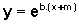 ocorreu mudança de inclinação, deixando fixo o ponto (-m,1) quando comparamos o gráfico com o anterior; essa mudança de inclinação foi provocada pelo fator b no expoente, que muda a base da função exponencial;
ocorreu mudança de inclinação, deixando fixo o ponto (-m,1) quando comparamos o gráfico com o anterior; essa mudança de inclinação foi provocada pelo fator b no expoente, que muda a base da função exponencial;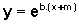 , multiplicada pelo coeficiente a;
, multiplicada pelo coeficiente a;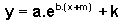 sofreu uma translação vertical de k unidades, pois, para cada abscissa, as ordenadas dos pontos do gráfico
sofreu uma translação vertical de k unidades, pois, para cada abscissa, as ordenadas dos pontos do gráfico O estudo dos gráficos das funções envolvidas auxilia na resolução de equações ou inequações, pois as operações algébricas a serem realizadas adquirem um significado que é visível nos gráficos das funções esboçados no mesmo referencial cartesiano.
Função exponencial e equações diferenciais
A maior importância das funções exponenciais nos campos das ciências é o fato de que essas funções são múltiplas de suas próprias derivadas:
Se a taxa de crescimento ou de decaimento de uma variável é proporcional ao seu tamanho, como é o caso de um crescimento populacional ilimitado, juros continuamente computados ou decaimento radiativo, então a variável pode ser escrita como uma função exponencial do tempo.
A função exponencial então resolve a equação diferencial básica
e é por essa razão comumente encontrada em equações diferenciais. Em particular a solução de equações diferenciais ordinárias pode freqüentemente ser escrita em termos de funções exponenciais. Essas equações incluem a equação de Schrodinger e a equação de Laplace assim como as equações para omovimento hormônico simples .ar]
Função exponencial no plano complexo
Quando considerada como uma função definida no plano complexo, a função exponencial retém as importantes propriedades:
- ez + w = ezew
- e0 = 1


para todos z e w. A função exponencial no plano complexo é uma função holomórfica que é periódica com o período imaginário 2πi que pode ser escrita como
- ea + bi = ea(cos b + isin b)
onde a e b são valores reais. Essa fórmula conecta a função exponencial com as funções trigonométricas , e essa é a razão que estendendo o logaritmo neperiano a argumentos complexos resultam na função multivalente ln(z). Nós podemos definir como uma exponenciação mais geral:: zw = ewln z para todos os números complexos z e w.
Isto é também uma função multivalente. As leis exponenciais mencionadas acima permanecem verdade se interpretadas propriamente como afirmações sobre funções multivalentes.
É fácil ver, que a função exponencial descreve qualquer curvano plano complexo a uma espiral logarítmica no plano complexo com centro em 0, nada como o caso de uma reta paralela com os eixos reais ou imaginários descrevem uma curva ou um círculo.r]
Função exponencial para matrizes e álgebras de Banach
A definição de função exponencial exp dada acima pode ser usada palavra por palavra para cada álgebra de Banach , e em particular para matrizes quadradas. Neste caso temos
- ex + y = exey
se xy = yx (deveríamos adicionar a fórmula geral envolvendo comutadores aqui)
- e0 = 1
- ex é invertível com inverso e-x
- a derivada da exp no ponto x é aquela descrição linear que transforma u em u·ex.
No contexto das álgebras de Banach não comutativas, como as álgebras de matrizes ou operadores no espaço de Banach ou de Hilbert, a função exponencial é freqüentemente considerada como uma função de um argumento real:
- f(t) = etA
onde A é um elemento fixo da álgebra e t é qualquer número real. Essa função tem importantes propriedades:
- f(s + t) = f(s)f(t)
- f(0) = 1
- f'(t) = Af(t)r]
Mapa exponencial nas álgebras de Lie
O "mapa exponencial" que passa uma álgebra de Lie a um grupo de Lie compartilha as propriedades acima, o que explica a terminologia. De fato, desde que R é uma álgebra de Lie de um grupo de Lie de todos os números positivos reais com multiplicação, a função exponencial para argumentos reais é um caso especial da situação da álgebra de Lie. Similarmente, desde que a álgebra de Lie M (n, R) de todas as matrizes reais quadradas pertence ao grupo de Lie de todas as matrizes quadradas invertíveis, a função para matrizes quadradas é um caso especial do mapa exponencial da álgebra de Lie.
Função Exponencial
Funções exponenciais são aquelas que crescem ou decrescem muito rapidamente.
Chama-se função exponencial a função ƒ:R→R+* tal que ƒ(x)= ax em que a € R, 0<a≠1.
O a é chamado de base e o x de expoente.
A função pode ser crescente ou decrescente a depender do valor da base. Se a base a for > 1, a função é crescente; Se a base a for um número real entre 1 e 0, (0<a< 1) a função é decrescente.
Chama-se função exponencial a função ƒ:R→R+* tal que ƒ(x)= ax em que a € R, 0<a≠1.
O a é chamado de base e o x de expoente.
A função pode ser crescente ou decrescente a depender do valor da base. Se a base a for > 1, a função é crescente; Se a base a for um número real entre 1 e 0, (0<a< 1) a função é decrescente.
- Sendo a > 0 e a ≠ 1, tem-se que ax=at↔ x = t;
- A função exponencial ƒ(x)=ax é crescente em todo seu domínio se, e somente se, a>1;
- A função exponencial ƒ(x)=ax é decrescente em todo seu domínio se, e somente se, 0<a<1;
- Toda função exponencial, isto é, ƒ(x)=ax com a € R+* e a ≠ 1 é bijetora;
Propriedades da Função Exponencial
A função exponencial é uma das mais importantes funções da matemática. Descrita como ex (onde e é a constante matemática neperiana, base do logarítmo neperiano), pode ser definida de duas maneiras equivalentes: a primeira, como uma série infinita; a segunda, como limite de uma sequência:
Aqui, n! corresponde ao fatorial de n e x é qualquer número real ou complexo.
O valor de e1 é aproximadamente 2.718281828
Se x é real, então ex é sempre positivo e crescente. Conseqüentemente, sua função inversa, ou logarítmo neperiano , ln(x), é definida para qualquer valor positivo de x. Usando o logarítmo neperiano, pode-se definir funções exponenciais mais genéricas, como abaixo:
- ax = exln a
Para todo a > 0 e  .
.
 .
.A função exponencial também gera funções trigonométricas (como pode ser visto na equação de Eulere para análises complexas), e as funções hiperbólicas. Então, tem-se que qualquer função elementar, exceto as polinomiais são criadas a partir da função exponencial.
As funções exponenciais "transitam entre a adição e a multiplicação" como é expressado nas seguintes leis exponenciais:



![\sqrt[c]{a}^b = a^{b \over c}](http://upload.wikimedia.org/wikipedia/pt/math/1/8/0/1801240b8ac015e6017d9c725dd99a94.png)
Assinar:
Postagens (Atom)



