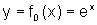 . Cada ponto do gráfico é da forma
. Cada ponto do gráfico é da forma 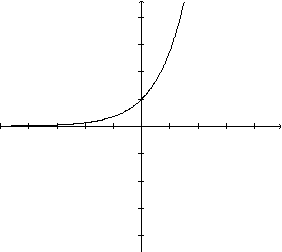
O domínio da função 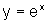 é
é 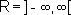 e a imagem é o conjunto
e a imagem é o conjunto 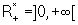 .
.
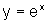 é
é 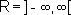 e a imagem é o conjunto
e a imagem é o conjunto 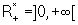 .
.O eixo horizontal é uma assíntota do gráfico da função. O que queremos aqui é descobrir como é o gráfico de uma função exponencial geral, quando comparado ao gráfico de 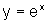 , a partir das transformações sofridas por esta função.
, a partir das transformações sofridas por esta função.
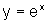 , a partir das transformações sofridas por esta função.
, a partir das transformações sofridas por esta função.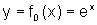 ?
?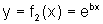 , quando a comparamos à função mais simples
, quando a comparamos à função mais simples 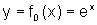 .
.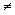 0
0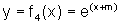 , onde m é um número real não nulo.
, onde m é um número real não nulo.CONCLUSÃO:
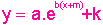
Conclusão: Podemos, portanto, considerar funções exponenciais do tipo
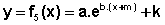 , onde os coeficientes a e b não são zero, examinando as transformações do gráfico da função mais simples
, onde os coeficientes a e b não são zero, examinando as transformações do gráfico da função mais simples 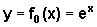 , quando fazemos, em primeiro lugar,
, quando fazemos, em primeiro lugar, 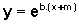 , depois
, depois 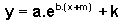 .
.Analisemos o que aconteceu:
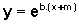 ocorreu mudança de inclinação, deixando fixo o ponto (-m,1) quando comparamos o gráfico com o anterior; essa mudança de inclinação foi provocada pelo fator b no expoente, que muda a base da função exponencial;
ocorreu mudança de inclinação, deixando fixo o ponto (-m,1) quando comparamos o gráfico com o anterior; essa mudança de inclinação foi provocada pelo fator b no expoente, que muda a base da função exponencial;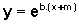 , multiplicada pelo coeficiente a;
, multiplicada pelo coeficiente a;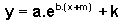 sofreu uma translação vertical de k unidades, pois, para cada abscissa, as ordenadas dos pontos do gráfico
sofreu uma translação vertical de k unidades, pois, para cada abscissa, as ordenadas dos pontos do gráfico O estudo dos gráficos das funções envolvidas auxilia na resolução de equações ou inequações, pois as operações algébricas a serem realizadas adquirem um significado que é visível nos gráficos das funções esboçados no mesmo referencial cartesiano.

Nenhum comentário:
Postar um comentário